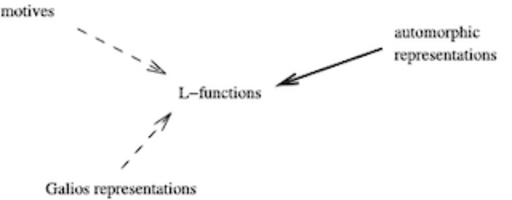
Geometry of Shimura varieties and arithmetic applications to L-functions
Raphaël Beuzart-Plessis, Yifeng Liu, Yichao Tian, Liang Xiao, Wei Zhang, and Xinwen Zhu have published two papers making significant progress on two major conjectures in arithmetic geometry: "Isolation of the cuspidal spectrum, with applications to the Gan-Gross-Prasad conjecture" by Beuzart-Plessis, Liu, Zhang, and Zhu, published in the Annals of Mathematics in 2021; and "On the Beilenson-Bloch-Kato conjecture for Rankin-Selberg motives" by Liu, Tian, Xiao, Zhang, and Zhu, published in Inventiones in 2022. The work originated in the AIM SQuaRE "Geometry of Shimura varieties and arithmetic application to L-functions" which met three times from 2017-2019.

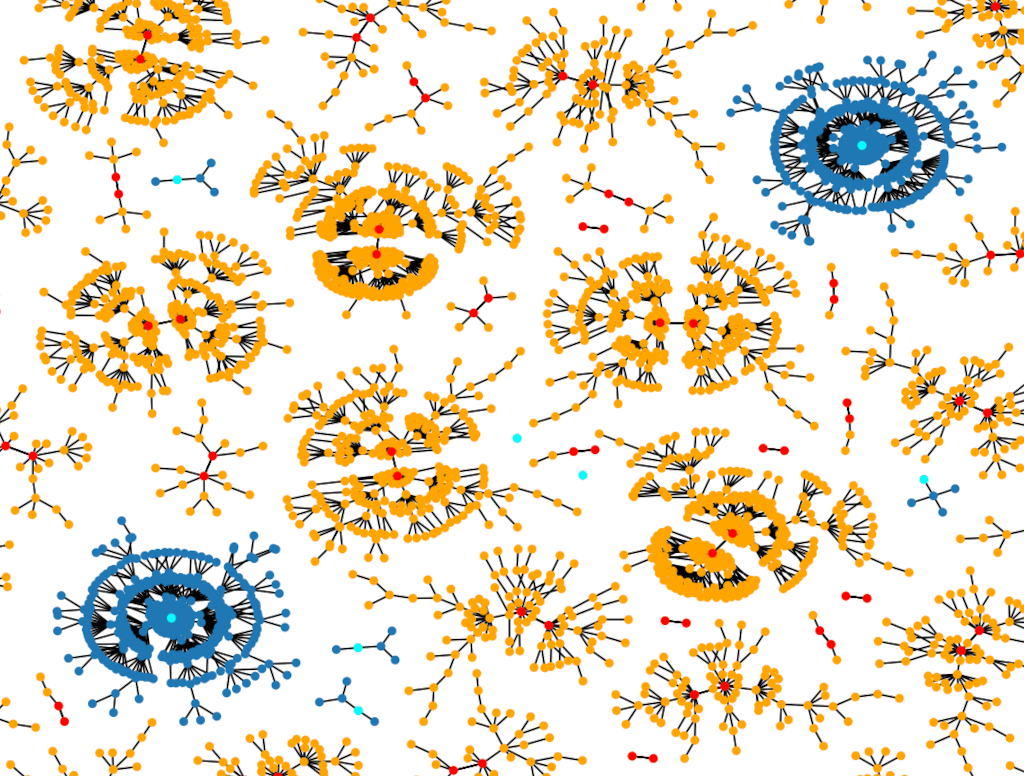
A Breakthrough in Global Dynamics on Graphs
A random network is a mathematical model used to study systems wherein interconnections form by chance. Nodes represent objects or entities; edges represent interactions.

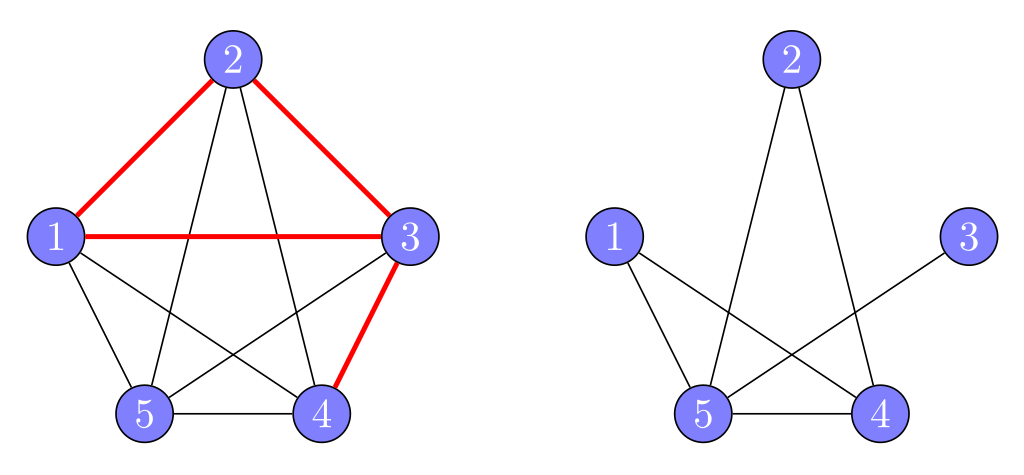
Percolation on Growing Graphs with Infinite-order Phase Transitions
Water percolates through sandstone. Coffee percolates to achieve a bold, strong brew. Ideas percolate over time.

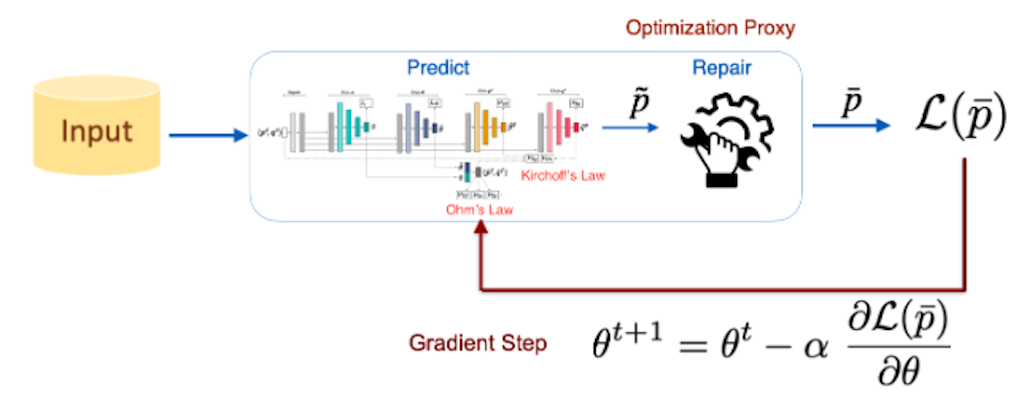
Uncertainty Quantification and Digital Twins Improve Autonomous Manufacturing
In the Spring of 2025, IMSI hosted a Long Program on “Uncertainty Quantification and AI for Complex Systems.” During the embedded Workshop on “Uncertainty Quantification for Material Science and Engineering,” Professor Wei Chen, Department of Mechanical Engineering, Northwestern University spoke about her work on digital twins applied to additive manufacturing.


Understanding Reticulate Evolution in the Genomic Era
Phylogenomics is the study of how biological entities, such as species or populations, evolve through time using genomic data. These relationships are traditionally represented using bifurcating trees where each point of split represents a speciation event and the branch represents a lineage over time. While the tree model depicts the historical relationships generally well, it sometimes oversimplifies the true complexity of evolution.


Sustainable plant harvest in fragmented landscapes
The members of the AIM SQuaRE “Sustainable plant harvest in fragmented landscapes” — Folashade Agusto, Benito Chen-Charpentier, Owusu Domfeh, Natali Hritonenko, Maria Leite, and Frank Owusu — set out to create mathematical models of the complex interactions between plant pathogens, harvest, and forest fragmentation.

The First Rigorous Validation of ‘Rattling’
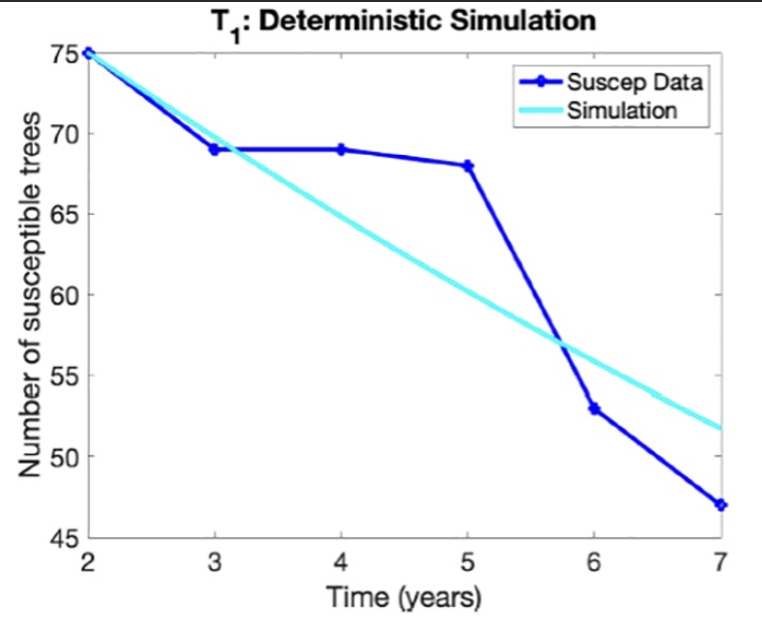
For years, working on an interdisciplinary project investigating order and collective behavior among complex systems — particles, ant colonies, flocks, robot swarms and the like — the computer scientist Dana Randall had heard about “rattling.”
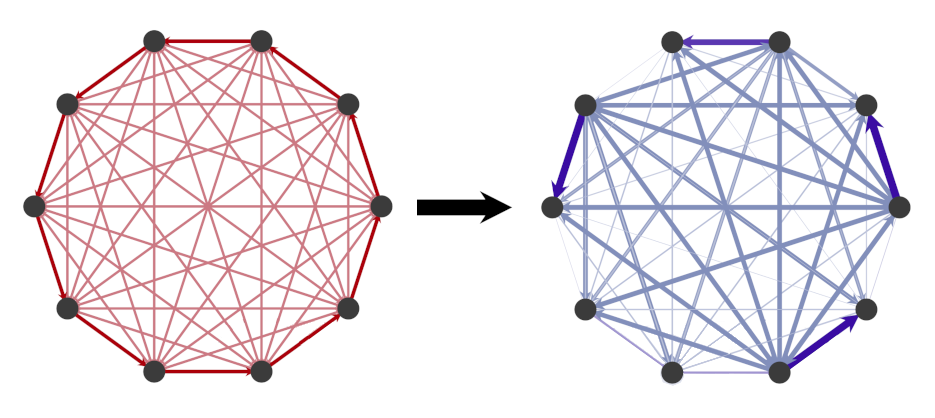

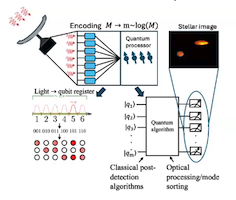
The Prospect for Using Quantum Enhanced Telescopes to Detect Exoplanets
IMSI hosted a Long Program on “Statistical Methods and Mathematical Analysis for Quantum Information Science” from September 16 thru December 13, 2024. This Long Program brought together mathematicians and statisticians who are collaborating with colleagues from physics, engineering, computer science, and other fields to solve major outstanding problems in the theory and applications of quantum information science. One of the embedded workshops was on Quantum Networks which included a talk by Johannes Borregaard on “Quantum networking for enhanced telescopes and tests of gravity.” This highlight will discuss the work of Borregaard and his colleagues on how a quantum enhanced telescope might be used for the detection of exoplanets.

When Do Ulrich Modules Exist?
In mathematics, studying objects through their representations is a well-tested path; the area representation theory is so named because it represents the study of a group, a ring, or any other algebraic structure via linear transformations, which are sometimes easier to work with. In algebraic geometry and commutative algebra, where the objects in question are varieties and their coordinate rings, the representations take the form of modules and sheaves.

Electrification and Green Energy Markets
As economies make the transition to green, renewable sources of electricity such as wind and solar, engineers, economists, energy producers and consumers, and regulators are struggling with how to integrate these new energy technologies into the grid. A major challenge is that wind and solar are only intermittently available and their availability may not coincide with periods or locations of high demand. To address the topic of electrification via renewables, the Institute for Mathematical and Statistical Innovation (IMSI) hosted a Long Program on “The Architecture of Green Energy Systems,” during the summer of 2024.