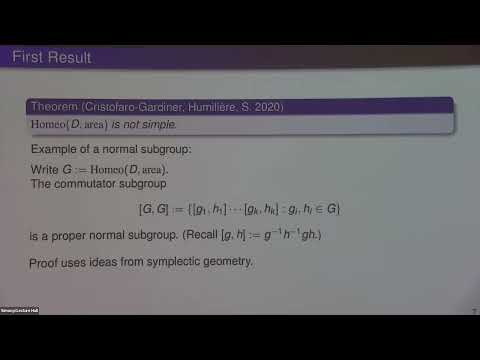
The algebraic structure of various groups of homeomorphisms and diffeomorphisms was studied extensively in the 1960s and 1970s, when it was shown that these groups are (mostly) simple. A notable open case concerned the group of area-preserving homeomorphisms of the two-dimensional disc. We explain how invariants arising from Floer theory—an infinite-dimensional analogue of Morse theory—together with methods from continuous symplectic topology, show that simplicity fails in this case. Symplectic Weyl laws play a central role in our story, as they permit the Calabi invariant—originally defined only in the smooth setting—to extend to area-preserving homeomorphisms. This, in turn, allows us to extend helicity, a conserved quantity of the three-dimensional Euler equations, from smooth volume-preserving flows to those that are merely continuous.