Written by Daniel Erman

The correspondence between graded algebra over a polynomial ring and the geometry of projective space has been a foundational piece of commutative algebra and algebraic geometry for well over a century.  This is a two-way bridge: geometric structures inspire new theorems on the algebra side, and algebraic structures inspire new theorems on the geometric side.

One question at the heart of two recent AIM workshops, “Syzygies and Mirror Symmetry” in Fall 2023 and "Homological mirror symmetry and multigraded commutative algebra” in Fall 2025, is how this algebra-geometry correspondence differs when one endows the polynomial ring with the extra structure of a multigrading.

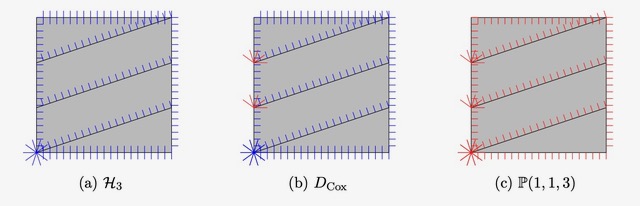
An answer begins with David Cox’s 1995 paper, which introduced what are now called Cox rings. He showed that the Cox ring of every smooth, projective toric variety \(X\) is a multigraded polynomial ring \(S\).  Cox’s work led to many theorems linking the algebra of the Cox ring with the geometry of the toric variety, but in some sense, most of the results went in one direction, using multigraded algebra to analyze toric geometry.

In retrospect, there is another reason that Cox’s correspondence worked better in the algebra \(\rightarrow\) geometry direction.  The correspondence between toric varieties and Cox rings is many-to-one, not one-to-one.  That is to say:  multiple toric varieties \(X_1, X_2, \dots , X_r\) can correspond to the same multigraded polynomial ring \(S\).  We can use algebraic tools for the polynomial ring \(S\) (graded ideals, graded modules) to study any of these toric varieties \(X_1, X_2, \dots , X_r\).

But what if we want to go in the opposite direction?  What if we want to utilize geometry to inspire new results in multigraded algebra?  There is “too much geometry”.  Which of the \(X_i\) should we look to as a guide for our new algebraic results?  Of course, the answer is that we need to utilize all of them, but this only begs another question: how do we study the “simultaneous” geometry of a collection of varieties \(X_1, \dots , X_r\)?

This question is at the heart of the recent paper “King’s Conjecture and Birational Geometry” by Ballard, Berkesch, Brown, Cranton Heller, Erman, Favero, Ganatra, Hanlon, and Huang.  The project focused on homological properties, and more specifically on derived categories.  With \(X_1, \dots , X_r\) as above, we considered the derived categories \(D(X_1), \dots , D(X_r)\) and we asked:  

We found inspiration from a surprising source.  Homological Mirror Symmetry is a deep connection between symplectic topology and algebraic geometry that was proposed by Kontsevich to explain mathematics arising from string theory.  Kontsevich’s Homological Mirror Symmetry Conjecture predicts the existence of mirror pairs \((X,\hat{X})\), where \(X\) is an algebraic variety and \(\hat{X}\) is a symplectic manifold, and there is an equivalence between \(D(X)\) and a Fukaya category of Lagrangian submanifolds on \(\hat{X}\). This program has been hugely successful for toric varieties, where the correspondence with partially wrapped Fukaya categories is understood in great detail.

If we push the categories \(D(X_1), \dots , D(X_r)\) through the mirror symmetry framework, they all have concrete descriptions on the symplectic side.  But whereas algebraic geometry is famously rigid, topology offers flexibility.  Specifically, the symplectic topology side offered a natural answer to the above question about how to synthesize these derived categories.  This led to new definitions on the algebraic side, and a new object of study—the Cox category.

Using this framework, we managed to modify and prove King’s Conjecture, which was a highly influential (though false) conjecture about derived categories of toric varieties.

Several of the collaborators on this project first met at the AIM workshop "Syzygies and Mirror Symmetry" where many discussions that led to the collaboration took place. In addition, the core collaborative group applied for and received an NSF FRG grant on this theme, and so the collaboration is ongoing. We are excited to see where these previously unpursued interactions between multigraded commutative algebra and symplectic topology will lead us.