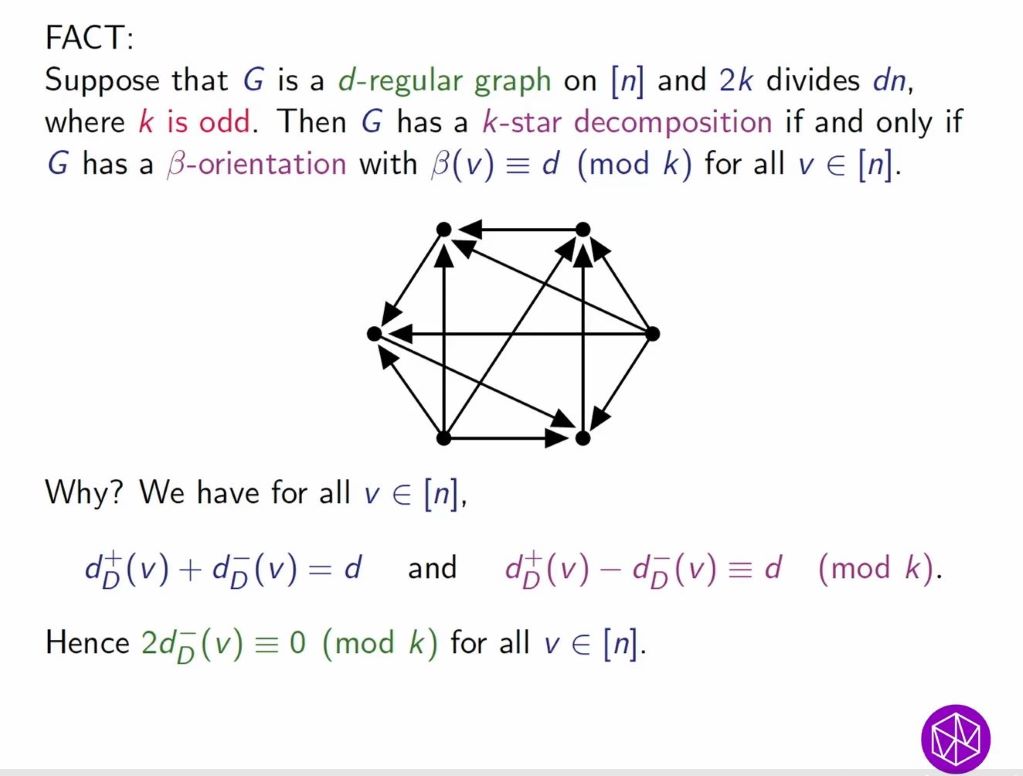
A $k$-star decomposition of a graph is a partition of the edge set into disjoint $k$-stars. Using the small subgraph conditioning method (SSCM), in 2018 Delcourt and Postle proved that with high probability, a random 4-regular graph has a 3-star decomposition. I will describe work to generalise this result. We have proved, again using the SSCM, that if a certain equation has a unique solution then with high probability, a random $d$-regular graphs has a $k$-star decomposition. We also prove that this sufficient condition holds whenever $k\leq d/2 + \log(d)/6$. There are connections with earlier work on beta-orientations which can be used to prove existence of $k$-star decompositions when $k \leq d/2$, while non-existence results can be obtained using a connection with independent sets in random regular graphs.