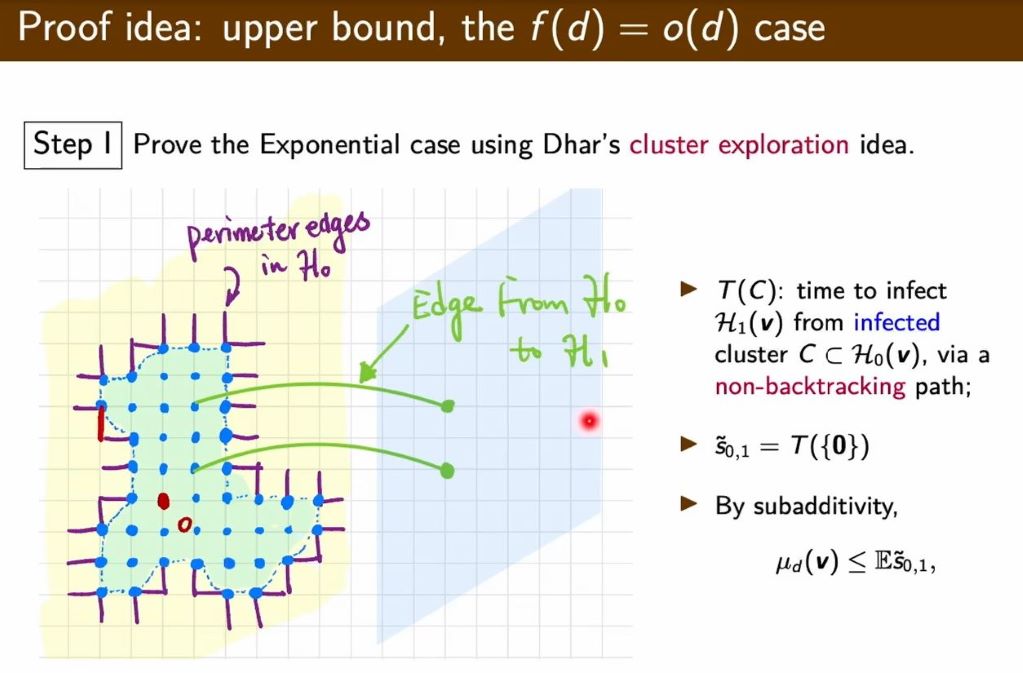
We prove high-dimensional asymptotics for the time constants in first-passage percolation (FPP) on $\mathbb Z^d$ along all diagonal-like directions $v=(1, 1, .., 1, 0, 0, …, 0)$ of $f(d)$ nonzero entries. We show that the behavior of the time constant is essentially the same as the axis directions if $f(d)=o(d)$ and is characterized by the Lambert W function if $f(d)~\alpha d$. Dhar’s cluster exploration idea was used in proving such results as well as deriving the moments of non-backtracking first-passage times.