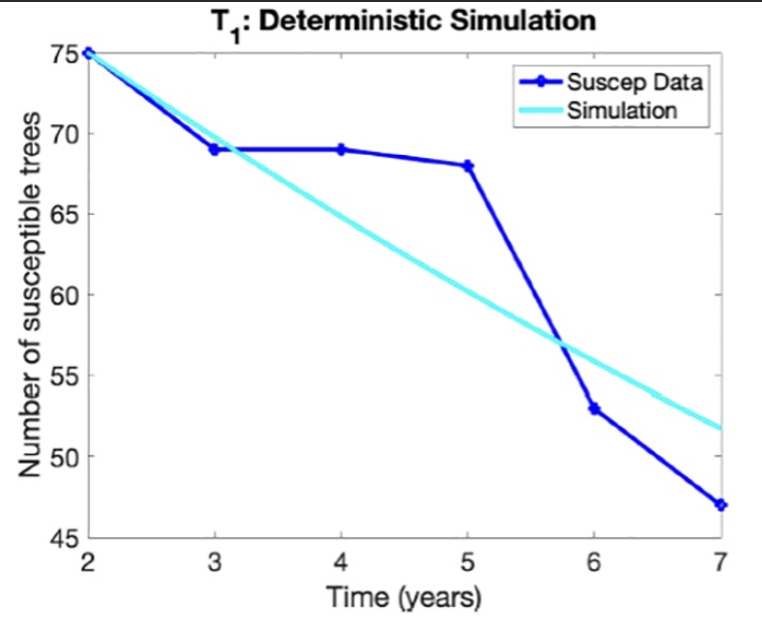
Sustainable plant harvest in fragmented landscapes
The members of the AIM SQuaRE “Sustainable plant harvest in fragmented landscapes” — Folashade Agusto, Benito Chen-Charpentier, Owusu Domfeh, Natali Hritonenko, Maria Leite, and Frank Owusu — set out to create mathematical models of the complex interactions between plant pathogens, harvest, and forest fragmentation.

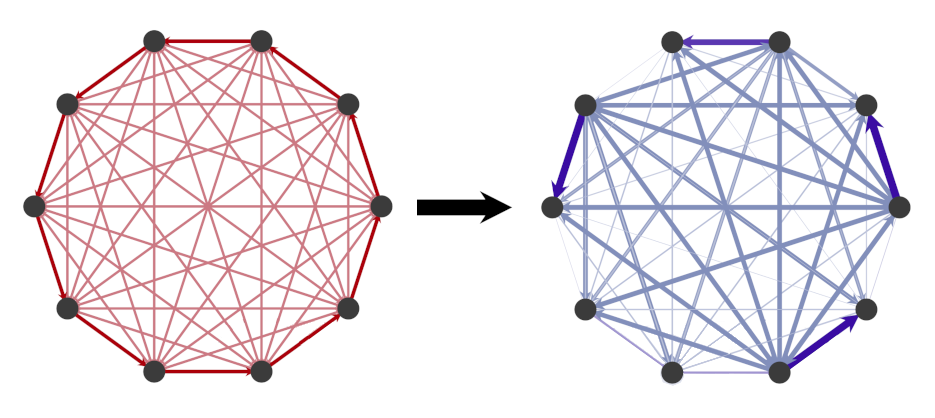
The First Rigorous Validation of ‘Rattling’
For years, working on an interdisciplinary project investigating order and collective behavior among complex systems — particles, ant colonies, flocks, robot swarms and the like — the computer scientist Dana Randall had heard about “rattling.”

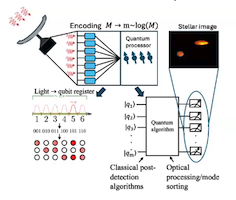
The Prospect for Using Quantum Enhanced Telescopes to Detect Exoplanets
IMSI hosted a Long Program on “Statistical Methods and Mathematical Analysis for Quantum Information Science” from September 16 thru December 13, 2024. This Long Program brought together mathematicians and statisticians who are collaborating with colleagues from physics, engineering, computer science, and other fields to solve major outstanding problems in the theory and applications of quantum information science. One of the embedded workshops was on Quantum Networks which included a talk by Johannes Borregaard on “Quantum networking for enhanced telescopes and tests of gravity.” This highlight will discuss the work of Borregaard and his colleagues on how a quantum enhanced telescope might be used for the detection of exoplanets.

When Do Ulrich Modules Exist?
In mathematics, studying objects through their representations is a well-tested path; the area representation theory is so named because it represents the study of a group, a ring, or any other algebraic structure via linear transformations, which are sometimes easier to work with. In algebraic geometry and commutative algebra, where the objects in question are varieties and their coordinate rings, the representations take the form of modules and sheaves.
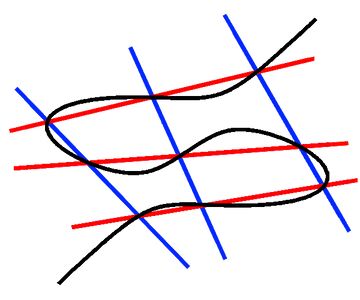

Electrification and Green Energy Markets
As economies make the transition to green, renewable sources of electricity such as wind and solar, engineers, economists, energy producers and consumers, and regulators are struggling with how to integrate these new energy technologies into the grid. A major challenge is that wind and solar are only intermittently available and their availability may not coincide with periods or locations of high demand. To address the topic of electrification via renewables, the Institute for Mathematical and Statistical Innovation (IMSI) hosted a Long Program on “The Architecture of Green Energy Systems,” during the summer of 2024.

IAS Researcher Debuts Counterexample to Viterbo’s Conjecture
Pazit Haim-Kislev has published a counterexample to Viterbo’s conjecture, demonstrating that some convex domains can achieve larger symplectic capacities than previously thought possible. With coauthor Yaron Ostrover, Haim-Kislev has discovered surprising features to the relationship between convex geometry and symplectic capacity. Their findings signal rich potential in further exploration of the unexpected ways these mathematical invariants behave...

New Momentum and Optimism at the Convergence of Geometry and Analysis
When contemplating degeneration and mess—such as wrinkles at points or cusps, or even wrinkling behavior that propagates to infinity on otherwise smooth surfaces known as manifolds—the Swiss-French mathematician Tristan Rivière, a professor at ETH Zurich, is upbeat and hopeful. “Understanding these degenerations is inspiring,” Dr. Rivière said.
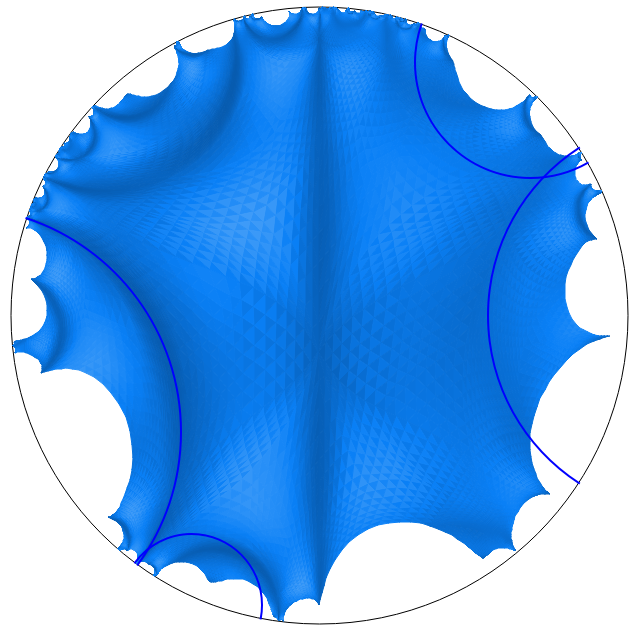

Ricci Flow, Redux
The much-vaunted Ricci flow equation was introduced by the mathematician Richard Hamilton in 1982. The equation is a tool: When applied to a manifold, a curved space in higher dimensions, the equation evolves the geometry of the space, making it smoother, more like a sphere. The Ricci flow is often compared to the heat equation, which describes how heat flows and distributes through space more evenly over time.
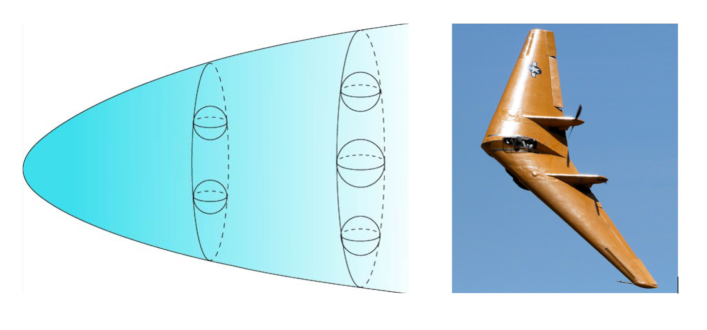

Algebraic Tools for Phylogenetic Networks
Phylogenetics is the field of mathematical biology concerned with recovering and describing evolutionary relationships between collections of taxa. The branching trajectory of evolution is often represented via a phylogenetic tree: vertices on the tree represent different taxa and taxa that are close to each other in the tree are evolutionarily close to each other. A major theme at the ICERM Fall 2024 program concerned the effort to move beyond trees.

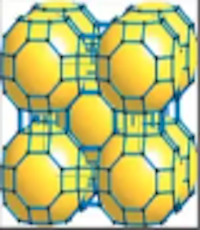
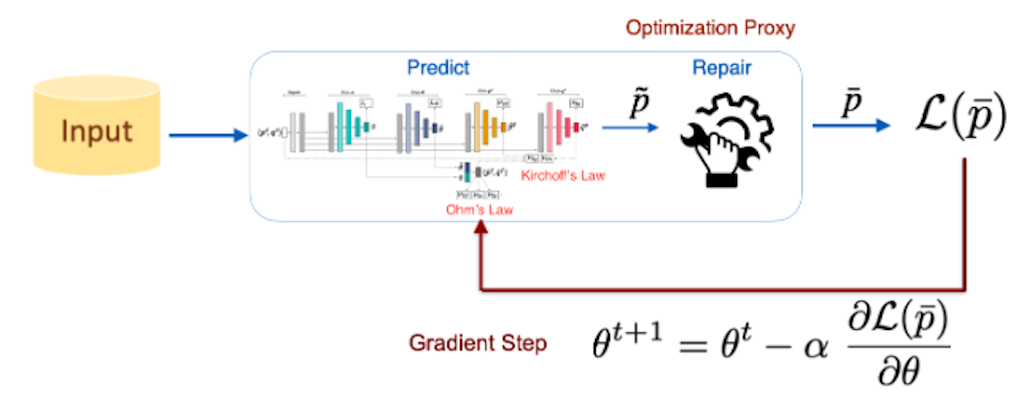
Machine Learning and Carbon Capture
Chemical engineers are teaming up with data scientists to use machine learning as a transformative technology in the discovery of new materials that can be used to capture the carbon dioxide produced by power plants. Their target are metal-organic frameworks – crystalline materials that act like sponges that can selectively absorb greenhouse gases in the flues of coal-burning and natural gas-burning power plants.